El MÉTODO DE LAS LÍNEAS DE TENSIÓN consiste en trazar un polígono definido por cuatro rectas, llamada ZONA ÚTIL, se encuentran infinitos pares ordenados (1⁄Po; eo ) que constituyen todos, soluciones del diseño que se realiza, para satisfacer las tensiones admisbles fijadas en el Estado Límite de Fisuración.

El método parte de transformar las ecuaciones que rigen las tensiones a nivel de las fibras extremas de la sección para los estados de carga más generales y frecuentes que actúan sobre la pieza, en rectas que deben ser trazadas sobre un plano cartesiano de abscisa 1⁄Po y ordenada eo.

La representación a escala de dichas rectas en aquel plano cartesiano puede llegar a definir un área cuyos puntos interiores satisfacen las tensiones admisibles planteadas. A continuación se describe detalladamente el procedimiento de cálculo según este método para el caso en que las cargas exteriores produzcan en la sección momentos flectores positivos, es decir, que traccionen las fibras inferiores, y en que se considerarán en sus valores modulares las características geométricas de la sección.

Sean las inecuaciones en las que se consideren las características geométricas correspondientes a la sección bruta de hormigón:

Estado [1]

FIBRA EXTREMA SUPERIOR:

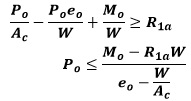
Como se explicó en las Hipótesis de Carga pueden presentarse dos situaciones en función de si lo más desfavorable son las solicitaciones en el centro o en el extremo de la viga. Si se presenta el 2do caso entonces se sustituye Mo por Mot y R1a por R1b.

FIBRA EXTREMA INFERIOR:

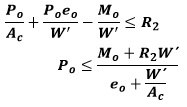
Si se realiza en ambas ecuaciones el siguiente cambio de variable:

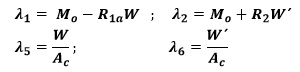
Las ecuaciones pueden plantearse en función de la excentricidad eo como:

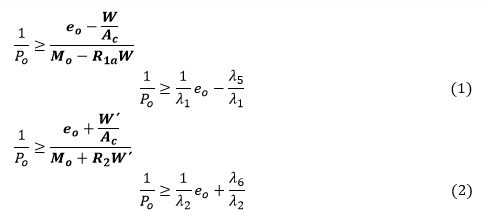
Estas ecuaciones ofrecen la carga máxima posible a aplicar a la sección sin que se superen las tensiones admisibles en la etapa de transferencia. Por tanto para una excentricidad dada la solución satisfactoria obliga a buscar una relación 1/Po por encima de las líneas de tensión condicionadas por las ecuaciones (1) y (2).

Estado [2]

FIBRA EXTREMA SUPERIOR:

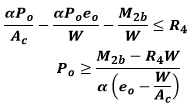
Pueden presentarse dos situaciones en función de si lo más desfavorable es la actuación de las cargas totales o de las cargas de larga duración. Si se presenta el 2do caso entonces se sustituye M2b por M2a y R4 por R3.

FIBRA EXTREMA INFERIOR:

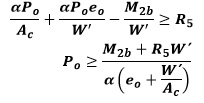
Se propone en este caso el siguiente cambio de variable:

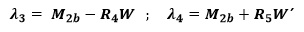
Demostrándose que las ecuaciones pueden plantearse en función de la excentricidad eo como:

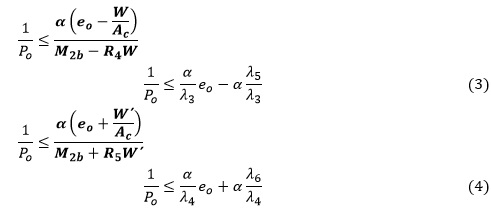
Estas ecuaciones ofrecen la carga mínima necesaria a aplicar a la sección sin que se superen las tensiones admisibles en la etapa de servicio. Por tanto para una excentricidad dada la solución satisfactoria obliga a buscar una relación 1/Po por debajo de las líneas de tensión condicionadas por las ecuaciones (3) y (4).

Se observa que todas las ecuaciones son de la forma (y=mx+b) y en consecuencia corresponden a líneas rectas, aunque de pendiente e intercepto con el eje de las ordenadas diferentes, lo que se muestra en la tabla siguiente:

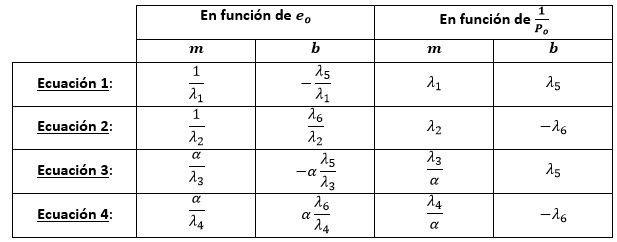
Las condiciones asociadas a las expresiones (1), (2), (3) y (4) representadas a escalas en el plano cartesiano (1⁄Po ; eo ), corresponden a rectas que delimitan un polígono que definirá una Zona Útil encerrada por dichas rectas, y cualquier punto que se seleccione dentro de esta superficie corresponde a una solución que cumple las tensiones admisibles fijadas, una vez que se lean a escala en dicha representación, los valores de 1⁄Po (define la fuerza inicial de pretensado Po) y de eo (define la posición del centroide de la distribución de los tendones que se requieren a partir de la fuerza Pe=αPo). En la figura se esquematiza la representación de estas rectas.

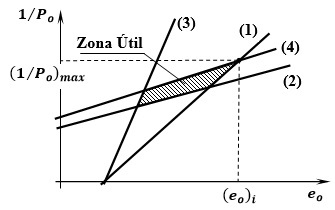
Sin embargo el simple trazado de las rectas que responden a las condiciones para cada tensión admisible no permite determinar la capacidad de la sección para soportar las cargas actuantes dentro de este rango. La detenida interpretación de los resultados resulta clave para la definición de un buen diseño.