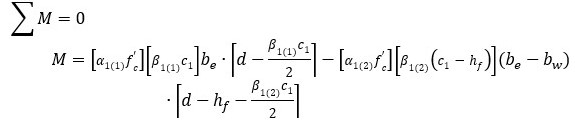Las secciones T son ampliamente empleadas por sus grandes ventajas para mejorar la resistencia a flexión. Si se desea deducir la curva de comportamiento de este tipo de sección utilizando el diagrama rectangular equivalente, es preciso distinguir para cada deformación εc' que se fije en la fibra de máxima compresión, las dos situaciones siguientes:

a) Si la altura del bloque de compresiones es menor que el espesor del ala de la sección, es decir, si 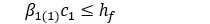el tratamiento es el mismo que se estudiara para las secciones rectangulares, solo que se debe considerar como ancho de la sección, el del ala comprimida, es decir,b=be.

b) Si la altura del bloque de compresiones es mayor que el espesor del ala de la sección, es decir, si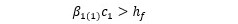

es conveniente recurrir al principio de superposición mediante el cual el área comprimida en la sección original se descompone en regiones rectangulares elementales. La Figura ilustra este principio.

En este último caso la descomposición consiste en restar a la contribución del rectángulo virtual de dimensiones (be;c1 ), la del otro rectángulo de dimensiones 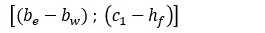ya que este en realidad no existe. Obsérvese que a la fibra más comprimida del primer rectángulo corresponde la deformación εc1', mientras que a la del segundo la deformación εc2'. Entre ambas deformaciones debe existir la siguiente relación de dependencia:

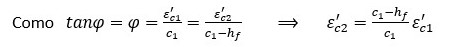
Puesto que las dos regiones en que ha quedado separada el área comprimida de la sección son rectangulares, se adoptan los coeficientes de transformación α1 y β1 correspondientes a esta tipología de sección, y para estimar la contribución en fuerza y momento de ambas regiones se procede de la manera siguiente:

COEFICIENTES DE TRANSFORMACIÓN:

REGIÓN 1: Para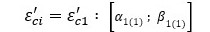

REGIÓN 2: Para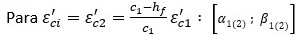

FUERZA:

REGIÓN 1: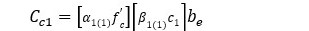

REGIÓN 2: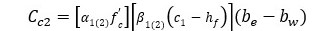

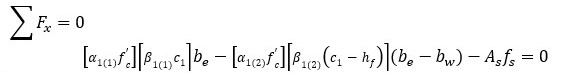
MOMENTO:

REGIÓN 1: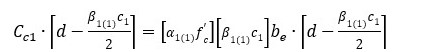

REGIÓN 2: