A continuación los procedimientos para el cálculo de cada punto para secciones rectangulares.

1. Rotura

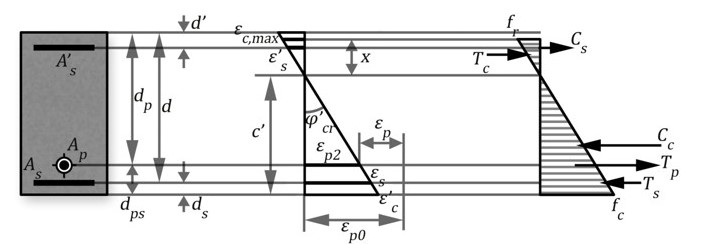
Es el mismo procedimiento que para el Hormigón Armado, considerar un valor de εc' máximo para el que se considera que la sección alcanza su capacidad soportante máxima. Entonces

En esta zona no es recomendable el empleo del modelo lineal, pero puede despreciarse el aporte del hormigón a tracción.

2. Fluencia

Se alcanza cuando el acero pretensado trabaja a su deformación de fluencia,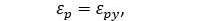 , conociendo que el efecto del pretensado provoca que este punto se alcance para curvaturas menores que en el Hormigón Armado.

Si existe refuerzo ordinario lo más frecuente es que el acero traccionado este fluyendo, pero para el comprimido situación para la que puede obtenerse la ecuación de equilibrio en función de la posición real de la línea neutra. Podría trabajarse con cualquier diagrama, pero habría que poner en función de la posición de la línea neutra no solo la tensión del refuerzo comprimido,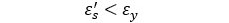 sino también los coeficientes .

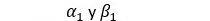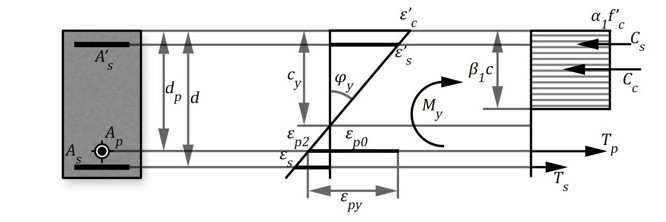
3. Fisuración

El momento de fisuración se alcanza cuando en la fibra inferior. Este valor puede determinarse fijando el valor de 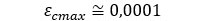o el valor de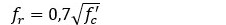

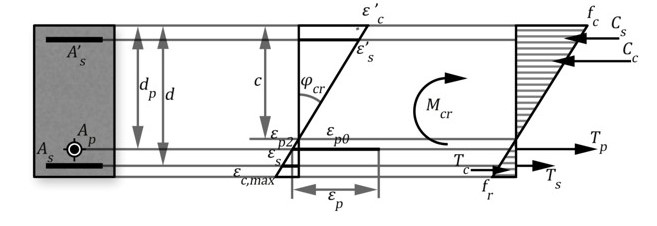
4. Curvatura cero

Se trata de obtener el momento flector que provoca la curvatura cero en la sección. La solución se logra obteniendo el valor de εc'. de la ecuación de compatibilidad. Aquí se calculará con diagrama lineal con el apoyo de la figura:

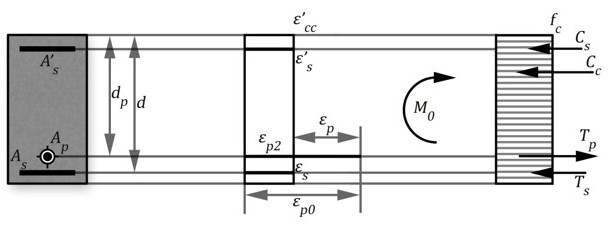
5. Momento cero

Para valores de momento menores de Mo la curvatura se invertirá, hasta llegar a su valor negativo mayor cuando el momento externo es cero, situación cercana al caso en que se tense el refuerzo pretensado y no actúe ni siquiera el peso propio de la vida.

Ante M=0, pueden presentarse dos casos:

1er caso: La sección no se fisura en su fibra superior pues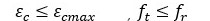

2do caso: La sección se fisura y deja de aportar una zona de la viga: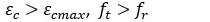

a) Calculo de φo para M=0 en sección NO FISURADA

El comportamiento de la sección se aprecia en la figura:

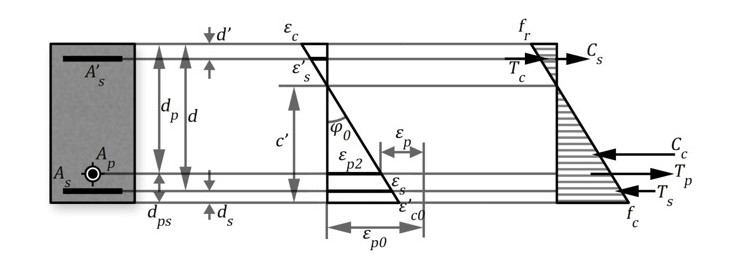
b) Calculo de Mcr' para la SECCION FISURADA

Como, en este caso, para M=0 la sección se fisura se presentará un valor de momento de fisuración para la fibra superior 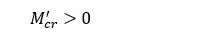Este momento se calcula cuando se alcanza ε_cmax en la fibra superior, como se aprecia en la figura.

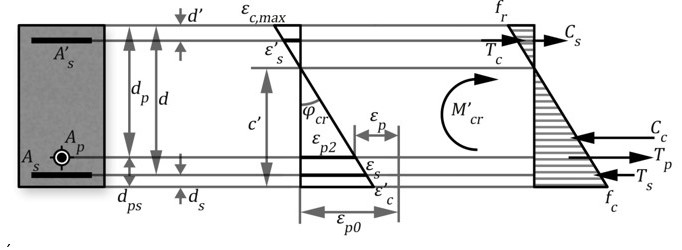
c) Calculo de φo para M=0 en la SECCION FISURADA

Esta resulta una solución compleja donde debe acudirse a tanteos, pues el diagrama de tensiones no se completa y son desconocidas todas las deformaciones de la sección, como se muestra en la siguiente figura: