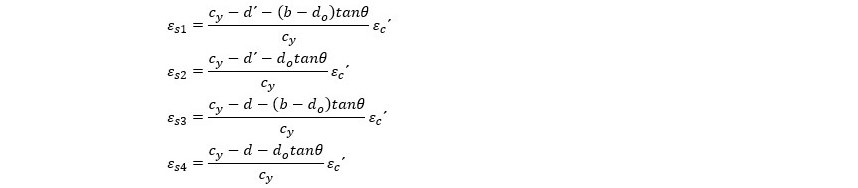Esta solicitación se produce en columnas de entramados donde en el pórtico secundario las cargas provocan excentricidades sobre estos debido a la propia concepción del esqueleto o por asimetrías en la acción de las cargas. Es típico en columnas de esquinas y estructuras especiales.

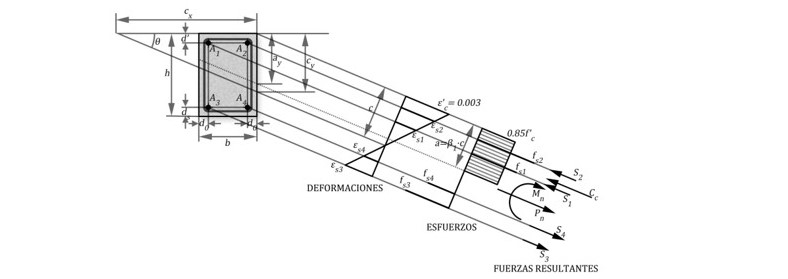
El análisis de la Flexión Compuesta biaxial o esviada se ilustra en la figura siguiente, donde la sección está sometida a una carga descentrada tanto en el eje x como en el y; siendo las excentricidades e_x y e_y respectivamente. En dicha figura se destacan los DIAGRAMAS DE INTERACCIÓN obtenidos para la flexo compresión recta en ambos ejes y esviada que ocurre en un angulo λ respecto al eje x este ángulo puede determinarse por:

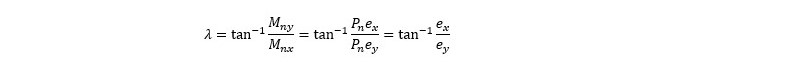
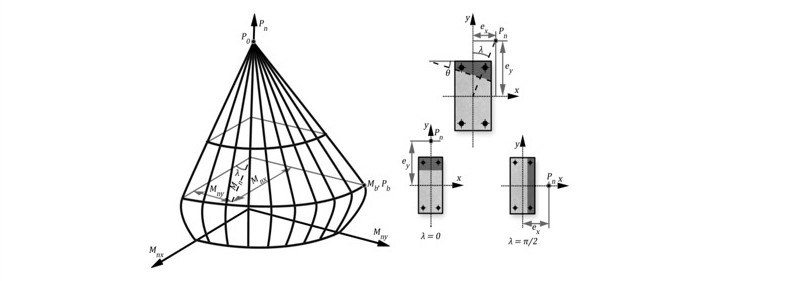
El diagrama obtenido para el caso recoge todas las combinaciones de carga y momentos flectores en ambos ejes que limitan la resistencia de la sección, como se explicó para la flexo compresión recta. También se destaca en la figura una superficie resistente para una carga P_n dada, conocida como CONTORNO DE CARGA o SUPERFICIE DE CONTORNO. Son dos formas de plantearse las zonas de resistencia de la sección.

Desde el punto de vista analítico el problema fundamental radica en determinar cual es la inclinación de la línea neutra θ, ya que no puede obtenerse una relación entre λ y θ, pues como regla no son iguales, ni se relacionan, como se muestra en la figura anterior. Las ecuaciones de equilibrio son:

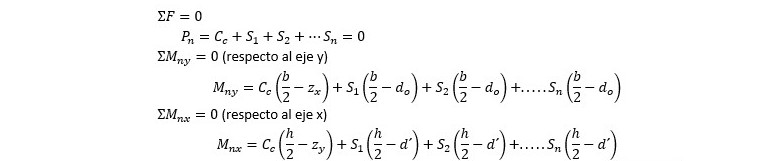
Donde z_x y z_y son las proyecciones sobre los ejes del brazo en la resultante del hormigón C_c.

Aporte del hormigón

Empleando el diagrama rectangular – equivalente en la figura anterior se muestra cómo actúa sobre la sección y como a partir del bloque comprimido puede obtenerse C_c

Donde A´ es el área comprimida del hormigón.

Pero pueden presentarse 4 formas de zona comprimida del hormigón en función de la magnitud y posición de la carga, y todo se trata de obtener el área comprimida y la posición del centroide. Esta problemática se ilustra en la figura.

Aporte del refuerzo

En la figura siguiente, se muestra el diagrama de deformaciones para una sección sometida a la flexión esviada y con 4 barras situadas en las esquinas, apoyo importante para determinar la tensión a que está sometido cada acero (f_si).

Considerando la proyección sobre el eje y

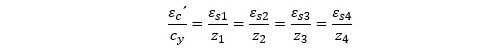
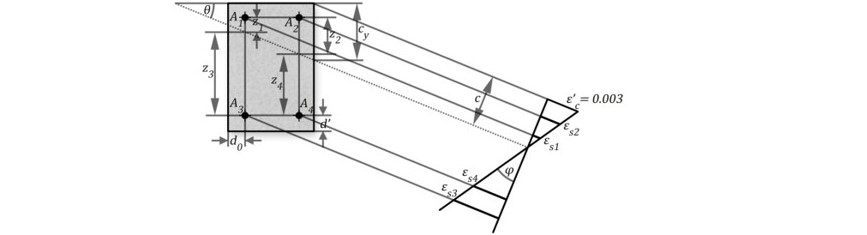
Donde:

Entonces: