A continuación se evalúan los procedimientos a seguir en el diseño de secciones a Flexo – compresión con Refuerzo Simétrico, es decir As=As'

1) No se requiere refuerzo por cálculo

La sección estaría situada en la Zona O y debe comprobarse que:

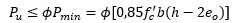
Entonces se coloca As=As'=Asmin

2) Tracción controlada. Zona 2. CASO 1

Los procedimientos de cálculo se dirigirán a determinar si el refuerzo más comprimido se agota o no.

Si se define la carga para la frontera de la tracción controlada en que c=0,375d,εs=0,005, ϕ=0,9,considerando que ambos refuerzos se agotan y se la llama P2:

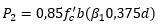
Entonces si:

3) Zona de Transición. Zona 3. CASO 2

Para combinaciones de carga que provocan que la sección trabaje en el rango de:

En este caso puede admitirse que ambos refuerzos trabajan a su máxima capacidad, solo que se introduce una reducción del coeficiente ϕ

4) Compresión controlada. Zona 4. CASO 3

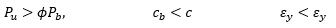
Debiéndose comprobar que:

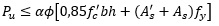
Valor máximo permitido por las normativas del ACI

Diseño para secciones en Tracción Controlada:

Siempre que Pu˂ϕP2 la sección a Flexo – compresión se acercará al trabajo de una viga y en esencia serán aplicables los mismos conceptos

Desde el punto de vista del diseño es importante precisar si el refuerzo más comprimido fluye o no,

CASO1a: fs'=fy

a) Determinar el valor de a y ϕ

Para P2 ≤ 0,9P2 conocido el valor de ϕ=0,9, puede obtenerse la profundidad del bloque rectangular por la ecuación de fuerzas y para As'=As:

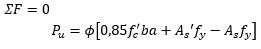
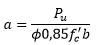
b) Cálculo de As'=As

De la ecuación de momento

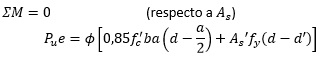
Donde:

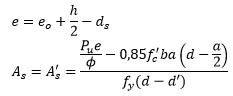
CASO 1b: fs'˂fy

a) Cálculo de a

Es necesario trabajar con las ecuaciones de equilibrio en función de c:

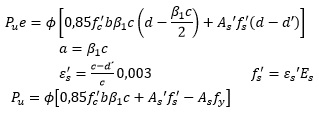
b) Cálculo de As'=As

De la ecuación de momento

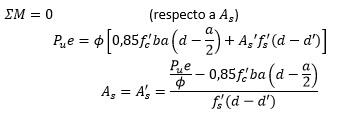
Diseño para secciones en la Zona de Transición:

Si la carga externa se encuentra en el rango en que:

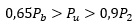
La sección estará en la Zona de Transición y ϕ es desconocido y tendrá valores entre 0,65 y 0,9, por lo que se hace necesario trabajar en la ecuación de fuerzas, poniéndola en función de c. Entonces, suponiendo que fs'=fy

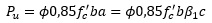
Por ejemplo para fy=300MPa, sustituyendo ϕ por la ecuación en función de c se obtiene:

Y finalmente de las expresiones de la tabla 10.7 puede obtenerse ϕ

En caso de que fs'˂fy, entonces debe calcularse c simultaneando las ecuaciones de equilibrio.

El cálculo del refuerzo se realiza de la misma forma que para la tracción controlada cuando fluye el acero más comprimido.

Diseño para secciones con Compresión Controlada:

Este es el caso en que Pu>ϕPb y de las ecuaciones generales:

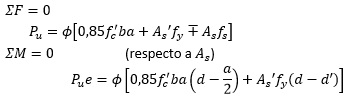
La solución de estas ecuaciones, calculando el valor real de la tensión del refuerzo menos comprimido As, se obtiene poniendo en función de c y simultaneando ambas ecuaciones, lo que trae como resultado una ecuación de 3er grado.